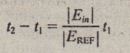The simplest type of ND converter employs a binary counter, a voltage comparator, and a D/A converter, as shown in Figure 19-13(a). Recall from Section 15-1 that the output of the voltage comparator is high as long as its v+ input is greater than its v· input. Notice that the analog input is the v+ input to the comparator. As long as it is greater than the v· input, the AND gate is enabled and clock pulses are passed to the counter. The digital output of the counter is converted to an analog voltage by the DAC, and that voltage is the other input to the comparator. Thus, the counter counts up untu its Outpllt has a value equal to the analog input. At that time, the comparator switches low, inhibiting the clock pulses, and counting ceases. The count it reached is the digital utput proportional to the analog input. Control circuitry, not shown, is used to latch the output and reset the counter. The cycle is repeated, with the counter reaching a new count ~lVl,JS “t)nal to whatever new value the analog input has acquired. Figure 19-13(b) illustrates the output of a 4-bit DAC in an ADC’bver several counting cycles when the analog input is a slowly varying voltage, The principal disadvantage of this type of converter is that

(a) Block diagram of an 8-bit ADC

the conversion time depends on them agnitude Of he analog input: the larger the input, the more clock pulses must pass to reach he pruper count. An 8-bit converter could require as many as 255 clock pulses to perform a conversion, so the counter type ADC is considered quite slow in comparison to other types we will study.
Tracking A/D Converter
To reduce conversion times of the counter-type ADC, the up counter can be replaced by an up/down counter, as illustrated in Figure 19-14. In this design.

the counter is not reset after each conversion. Instead, it counts “up or do\’. n from its last count to its new count. Thus, the total number of clock pulses required to perform a conversion is proportional to the change in the analog input between counts rather than to its magnitude. Since the count more or less keeps up -ith the changing analog input, the type of ADC is called a tracking converter. A disadvantage of he design is that the count may oscillate up and down from a fixed count when t ie anal g input is constant.
FLASH A/D CONVERS
The fastest type of AID converter is called the flash (or simultaneous, or parallel) type. As shown for the 3-bit example in Figure 19-15, a reference voltage is connected to a voltage divider that divides it into 7 (2″ – I) equal-increment levels. Each level is compared to the analog input by a voltage comparator. For any given analog input, one comparator and all those below it will have a high output. All comparator outputs are connected to a priority ellcoder. A priority encoder produces a hiu.u y output corresponding to the input having the highest priority, in this case, the one representing the largest voltage level equal to or less than the analog

input. Thus, the binary output represents the voltage that is closest in value to the analog input
THE DUAL-SLOPE (INTEGRATING) ADC
Recall from Chapter 14 that the output of an integrator is a ramp when the input is a ffixedlevel (Figure 14-33). The slope of the ramp is ±E ••IRI C, where E”, is the input voltage that is integrated and RI and C an: the fixed components of the integrating operational amplifier. Since RI and C arc fixed, the slope of the ramp is directly dependent on the value of EiH• If the ramp is allowed to continue for a fixed time. the voltage it reaches in that time depends on the slope of the ramp and hence on the vslue of Em. The basic principle of the integrating ADC is that the voltage reached ‘by the ramp controls the length of time that a binary counter is allowed to count. Thus, a binary number proportional to the value of E;” is obtained. In the dual-slope ADC, two integrations are performed, as described next.
Figure 19-17(a) shows a functional block diagram of the dual slope AOC. Recall that the integrating operational amplifier inverts, so a positive input generates a negative-going ramp and vice versa. A conversion begins with the switch connected to the analog input. Assume that the input is negative, so a positive-going ramp is generated by the integrator. As discussed earlier, the ramp is allowed to continue for a fixed time, and the voltage it reaches in that time is directly dependent on the analog input. The fixed time is controlled by sensing the time when the counter reaches a specific count. At that lime, the counter is reset and control circuitry causes the switch to be connected to a reference voltage having a polarity opposite to that of the analog input-in this case, a positive voltage. As a consequence. the output of the integrator becomes a negative-going ramp, beginning from the positive value it reached during the first integration. Since the reference voltage is fixed, so is the slope of the negative-going ramp., When the negative-going ramp reaches o V, the voltage comparator switches, the clock pulses are inhibited, and the counter ceases to count. The count it contains at that time is proportional to the time required for the negative-going ramp to reach 0 V, which is proportional to the positive voltage reached in the first integration. Thus, the binary count is proportional
to the value of the analog input. Figure 19-17(b) shows examples of the ramp waveforms generated by a small analog input anti by a large analog input. Note that the slope of the positive-going camp is variable (depending on E;n), and the slope of the negative-going ramp is fixed. The origin of the name dllal-sllfJe’is now apparent.
One advantage of the dual-slope converter is that its accuracy depends neither on the values of the integrator components RI’ and C (lor upon any long-term changes that may occur in them. This fact is demonstrated by examining the equations governing the times required for the two integrations. Since the slope of the positive-going ramp is E;,,/ RI C, the maximum voltage V M reached’ by the ramp in time II is

Cancelling RI C on both sides and solving for 12- II gives
Since the counter contains a count proportional to (2 – II (the time required for the negative-going ramp to reach 0 V) and II is fixed, equation (19-17) shows that the count is directly proportional to E••, the analog input. Note that this expression does not contain RI or C, since those quantities cancelled out in (19-16). Thus, accuracy does not depend on their values. Furthermore, accuracy does not depend
on the frequency of the clock. Equation (19-17) shows that accuracy does depend on EREF, so the reference voltage should be very precise.
An important advantage of the dual-slope AID converter is that ‘the integrator suppresses noise. Recall from equation (14-46) that the output of an integrator r • has amplitude inversely proportional to frequency. Thus, high-frequency noise components in the analog input are attenuated. This property makes it useful for . instrumentation systems, and it is widely used for applications such as digital voltmeters. However, the integrating ADC is not particularly fast, so its use is restricted to signals having low to medium frequencies.