An oscillator is a device that generates a periodic, ac output signal without any form of input signal required. TIle term is generally used in the context of a sine-wave signal generator, while a square-wave generator is usually called a multioibrator. A function generator is a laboratory instrument that a user can set to produce sine, square, or triangular waves, with amplitudes and frequencies that can be adjusted at will. Desirable features of a sine-wave oscillator include the ability to produce a low distortion (“pure”) sinusoidal waveform, and, in many applications, the capability of being easily adjusted so that the user can vary the frequency over some reasonable range.
Oscillation is: a form of instability caused by feedback that regenerates, or reinforces, a signal that would otherwise die out due to energy losses. In order for the feedback to be regenerative. it must satisfy certain amplitude and phase relations that we will discuss shortly. Oscillation often plagues designers and users of high-gain amplifiers been. Use of unintentional feedback paths that create signal regeneration at one or more frequencies. By contras • an oscillator is designed to have a feedback path with known characteristics, so that a predictable oscillation will occur at a predetermined frequency
The Barkhausen Criterion
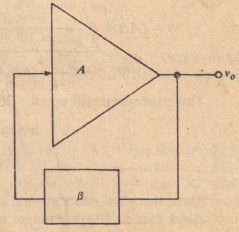
We have stated that an oscillator has no input per se, so the reader may wonder what we mean by “feedback”-feedback to where? In reality, it makes no difference where, because we have a closed loop with no summing junction at which any external mp t i added. Thus, we could start anywhere in the loop and call ‘that point both the “input” and the “output”; in other words, we could think of the “feedback” path as the entire path through which signal flows in going completely around the loop. However, it is customary and convenient to take the output of an amplifier as a reference point and to regard the Iecdbackjpath as that portion of the loop that lies between amplifier output and amplifier input. This viewpoint is illustrated in Figure 14-41, where we show an amplifier having gain A and a feedback I”ltB ~~.l1g gain . p. is t n .:’!~I feedback ratio that specifics the portion of amplifier output voltage fcrl hack to amplifier input. Every oscillator must have an amplifier, or equivalent device, that supplies energy (from the de supply) to replenish resistive losses and thus sustain oscillation.
In order for the system shown in Figure 14-41 to osc;~\’.~’. l\lc loop gain “/3 must satisfy the Barkhausen criterion, namely,
Imagine a small variation in signal level occurring at the input to the arn rlifier, perhaps due to noise. The essence of the Barkhausen criterion is that this variation will be reinforced and signal regeneration will occur only if the net gain around the loop. beginning and ending at the point where the variation occurred, is unity. It is important to realize that unity gain means not only a gain magnitude of I, hut also an in-phase signal reinforcement. Negative feedback causes signal cancellation because the feedback voltage is out of phase. By contrast, the unity loop-gain criterion for oscillation is often called positive feedback.
To understand and apply the Barkhausen criterion, we must regard both the gain and the phase shift of AJ3 asfunctions offrequency. Reactive elements, capacitance in particular, contained in the amplifier and/or feedback cause the gain magnitude and phase shift to change with frequency. In general, there will be only one frequency at which the gain magnitude is unity and at which, simultaneously, the total phase shift is equivalent to 0 degrees (in phase-a multiple of 360°). The system will oscillate at the [requency that satisfies those conditions. Designing an oscillator amounts to selecting reactive components a id incorporating them into circuitry in such a way that the conditions will be satisfied at a predetermined frequency.
To show the dependence of the loop gain Af3 on frequency, we write Af3(jw), a complex phasor that can be expressed in both polar and rectangular form: The gain of a certain amplifier as a function of frequency is A(jw) == -16 X 1()1’/ . A feedback path connected mound it has f3(jw} = 1O~/(2 X 103 + jW)2. Will the system oscillate? If so, at what frequency?
Example 14-15 illustrated an application of the polar form of the Barkhausen criterion, since we solved for IAf3 and then determined the frequency at which that angle equals -360°. It is instructive to demonstrate how the same result can, be obtained using the rectangular form of the criterion: A{3 = 1 + jO. Toward that end, we first expand the denominator:
To satisfy the Barkhauscn criterion, this expression for Af3 must equal I. We therefore set it equal to I and simplify:
In order for this expression to equal 0, both the real and imaginary parts must equal O. Setting either part equal to 0 and solving for t» will give us the same result we obtained before
This result was obtained with somewhat more algebraic effort than previously. In some applications. it is easier to work with the polar form than the rectangular form. and ill others. the reverse is true.