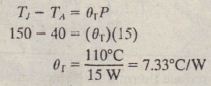Conduction Radiation and Convection
Heat transfer takes place by one or more of three fundamental mechanisms: conduction radiation, and convection as illustrated in Figure 16-3. Conduction occurs when the energy that the atoms of a material acquire through heating is transferred to adjacent less energetic atoms in a cooler region of the material. For example conduction is the process by which heat flows from the heated end of a metal rod toward the cooler end and the process by which heat is transferred from the heating

Examples illustrating heat transfer hy conduction radiation. and connection
element of a stove to a pan, and from the pan to t ie water it contains. Heat radiation is similar to other forms of radiation because no physical medium is required between the heat source and its destination. For example heat is transferred by radiation through space from the sun to the earth. Convection occurs when a
physical medium that has been heated by conduction or radiation moves away from the source of heat i.e., is displaced by a cooler medium so more conduction or radiation can occur. Examples include forced convection where a fan is used to push air past a heated surface and natural convection where heated air rises and
is replaced by cooler air from below.
Semiconductor devices are cooled by all three heat-transfer mechanisms. Heat is conducted from a junction, through the semiconductor material through the case and into the surrounding air. It-is radiated From the surface of the case. Heating of the surrounding air creates air flow around the device so convection cooling occurs. Various measures are taken to enhance heat transfer by each mechanism. To improve conduction, good physical contact is made between a junction and a device’s metal case or enclosure. In fact in many power transistors the collector is in direct contact with the case so the two are electrically the same as well as
being at approximately the same temperature. To improve the conduction and radiation of heat from the case to the surrounding air, power devices are often equipped with heat sinks. These are attached to the device to be cooled and conduct heat outward to metal fills that increase the total surface area from which conduction
and radiation into the air can take place. See Figure 16-4. Finally convection cooling is enhanced by the use of fans that blow cool air past the surface of the case and/or the heat sink
Thermal Resistance
Heat flow by conduction is very much like the conduction of electrical charge i.e. current. Recall mat current is the rate of flow of charge and is proportional to the

difference in voltage across a resistance. Similarly, power is the rate of flow of heat energy and is proportional to the difference in temperature across the region through which heat is conducted. We can regard any impediment to heat flow as thermal resistance O.Thus the rate of now of heat (i.e., power) is directly proportional to
temperature difference and inversely proportional to thermal resistance:

Insulating materials like wool have large thermal resistances and metals have small thermal resistances. Note the similarity of equation 16-5 to Ohm’s law: I = (V2 – VI)/R. Solving for 8 in (16-5) we obtain the following equivalent relation that allows us to de:·mine the units of thermal resistance

In a power amplifier heat is transferred through different types’ of materials and across boundaries of dissimilar materials each of which presents different values of thermal resistance. These are usually treated like series electrical circuits so thermal resistances are added “‘H”‘1i computing the total heat flow through the system or the temperatures at various points in the system
Example 16-2
The collector-base junction of a certain transistor dissipates 2 W. The thermal resistance from junction to case is 8°C/W, and the thermal resistance from case to .’ air is 20°C/W. The free-air temperature (ambient temperature) is 25°C.
1. What is the junction temperature?
2. What is the case temperature?
Solution
1. The total thermal resistance between junction and ambient is the sum of that from junction to case and that from case to ambient: OT = OlC + 8CA = 8°C/W + 20°C/W = 28°C/W. Therefore, by equation 16-5, with T2 = T, = junction temperature and TI = TA = ambient temperature
2. The rate of heat flow P is constant through the series configuration so
To reduce thermal resistance and improve heat conductivity a special silicone grease is often used between contact surfaces such as between the case and heat sink. Mica washers are used to isolate the case and heat sink electrically when the case is electrically common to one of the device terminals such as a collector. The washer creates additional thermal resistance in the heat flow path between the case and heat sink and may have to be taken into account in heat-flow computations
The values of the thermal resistance of various types of heat sinks washers and metals can be determined from published manufacturers’ data. The data are often given in terms of thermal resistivity p (OC . in.lW or °C . rn/W), and thermal resistance is computed by
where

For example. a typical value of p for mica is 66″C . in/W, so a O.OD2-il.-thick mica washer having a surface area of 0.6 in.’ will have a thermal resistance of
Example 16-3
The maximum permissible junction temperature of a certain power transistor is 150°C. It is desired to operate the transistor with a power dissipation of 15 W inan ambient temperature of 40°C. The thermal resistances are as follows
1.. Determine whether a heat sink is required for this application.
2. If a beat sink is required, determine the maximum thermal resi lance it can have. Assume that a mica washer having thermal resistance Ow = 0.5°C/W must be used between case and heat sink
Solution
Since the junction temperature, 197.5°C, will exceed the maximum permissible value of 150°C under the given conditions, a heat sink must be used to reduce the total thermal resistance.
2. Setting TJ equal to its maximum permissible value of 150″C, we can solve for the maximum total thermal resistance: